上一篇我們示範了最近鄰插值及雙線性插值的效果比較，現在要來用python講解這兩個演算法實際運作的方式，藉由最簡單的影像縮放方法來更了解數位影像如何提升解析度。

一幅數位影像就像是一個函數，當對它放大或縮小時會映射到另一個函數，新函數（影像）的定義域裡每個點（像素）都會對應到原始函數的某處。

org_x = new_x * (org_width/new_width)
org_y = new_y * (org_height/new_height)

舉例來說，當一幅3x3的影像F(x, y)放大為4x4的影像Q(x, y)時，Q(1, 2)即對應到F(x=1(3/4), y=2(3/4)) = F(0.75, 1.5)。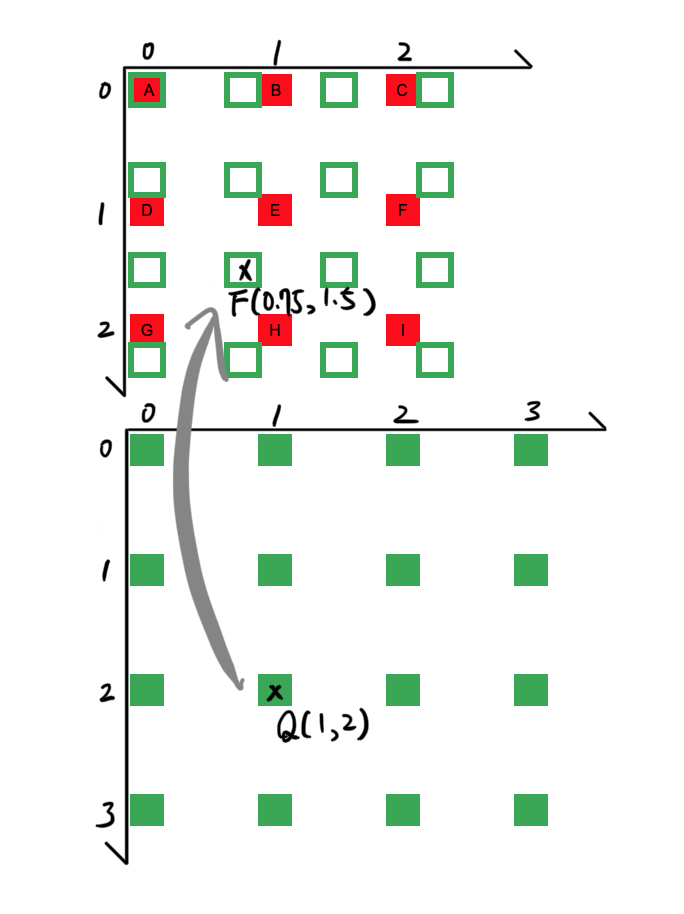

不過數位影像不可能在(0.75, 1.5)有值，因此必須靠演算法估算出這個值。
以上一篇所提到的最近鄰插值為例，F(0.75, 1.5)的值會直接對應最鄰近像素的值。python語言表示如下

org_x = np.clip(int(np.around(org_x)), 0, org_width-1)
org_y = np.clip(int(np.around(org_y)), 0, org_height-1)

np.around會四捨五入到鄰近的座標點，np.clip確保不會超出原始影像的座標。
因此在最近鄰插值下F(0.75, 1.5)的值等於F(1, 2)的值。

實際測試用python寫的最近鄰插值來對CV女神Lenna放大2倍

def nearest_neighbour(org, new_shape):
    org_height, org_width = org.shape[0], org.shape[1]
    new_height, new_width = new_shape[0], new_shape[1]

    new = np.zeros(shape=new_shape, dtype=np.uint8)
    for new_x in range(new_width):
        for new_y in range(new_height):
            org_x = new_x * (org_width/new_width)
            org_y = new_y * (org_height/new_height)

            if org_x-0.5 == np.floor(org_x): org_x = org_x+0.01
            if org_y-0.5 == np.floor(org_y): org_y = org_y+0.01
            
            org_x = np.clip(int(np.around(org_x)), 0, org_width-1)             
            org_y = np.clip(int(np.around(org_y)), 0, org_height-1)
            new[new_y, new_x, :] = org[org_y, org_x, :]
    return new

嗯，效果就如我們預期的差。下一篇我們會實作雙線性插值，來比較兩種提升解析度方法的成效。

Google colab代碼演示：https://colab.research.google.com/drive/1YOXaqP8oBV584DEefbNT0MvdWdiVXjOn?usp=sharing